Speed of Sound Wave In A Fluid-

 

Before you go through this article, make sure that you have gone through the previous article on Speed of Sound Wave in Fluids.

 

We have learnt that-

• The speed of sound wave through a fluid is determined by the bulk modulus and density of the fluid.
• The speed of sound wave through a fluid is given by the formula-

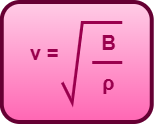
• A given solid or a liquid has a fixed value of bulk modulus but so is not the case for gases.
• The value of bulk modulus of a gas depends on the process.

 

In this article, we will learn about Newton’s Formula for speed of sound in a gas.

 

Newton’s Formula For Speed of Sound In A Gas-

 

As a sound wave travels through air, the segments of the medium are subjected to a series of compressions and rarefactions.

 

Newton suggested that-

• The temperature variations in an element due to compressions and rarefactions are negligible.
• When a small element of air gets compressed, the amount of heat produced during compression is lost to the surroundings and thus the temperature remains constant.
• Similarly, when a rarefaction arrives, the amount of heat lost during rarefaction is gained from the surroundings and thus the temperature again remains constant.
• Such a process in which volume and pressure of a gas changes but temperature remains constant is called an isothermal process.

 

In such a process, the gas satisfies the equation-

 

 

It means the bulk modulus of an ideal gas in an isothermal process is equal to the pressure of the gas.

 

Substituting in the formula v = √(B/ρ), we get-

 

This formula is called as Newton’s formula for the speed of sound in a gas.

 

Calculating Speed of Sound Using Newton’s Formula-

 

Let us now use Newton’s formula to calculate the speed of sound in air at NTP.

 

At NTP, we have-

• P = 1 atm = 1.013 x 10⁵ Pa
• ρ = 1.293 kg/m³

 

Substituting in the formula, we have-

 

Experimentally, the speed of sound in air at NTP is 332 m/s.

Thus, the value of speed of sound calculated using Newton’s formula is less than the experimental value of the speed of sound.

 

Error in Newton’s Formula-

 

Difference between the experimental value of speed of sound in air and the value calculated using Newton’s formula

= 332 – 280

= 52 m/s

Thus, percentage error in the calculated value is given by-

 

 

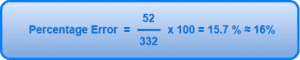
Such a large error could not be taken as an experimental error. Newton put forward a number of arguments to explain the above discrepancy but none of them was satisfactory.

Later, a French mathematician & physicist, Laplace explained the exact cause of discrepancy.

 

Test Your Concepts-

Newton’s Formula For Speed of Sound Wave in Gas

 

Next Article-

Laplace’s Correction

 

Get more notes & other study material of the Chapter Waves.