Rutherford’s Alpha Particle Scattering Experiment-

 

Before you go through this article, make sure that you have gone through the previous article on Rutherford’s alpha particle scattering experiment.

 

We have learnt that-

• In alpha particle scattering experiment, the alpha particles were bombarded on thin gold foil.
• After the collision, the alpha particles were scattered in different directions.

 

In this article, we will learn about distance of closest approach.

 

Distance of Closest Approach-

 

• Consider an α-particle moves directly towards the center of an atom.
• As it approaches the positive nucleus, it experiences a coulombic repulsion and its kinetic energy gets progressively converted into electrostatic potential energy.
• At a certain distance r₀ from the center of the nucleus, the α-particle stops for a moment and then begins to retrace its path i.e. it is scattered through an angle of 180°.
• The distance r₀ is called the distance of closest approach.

 

 

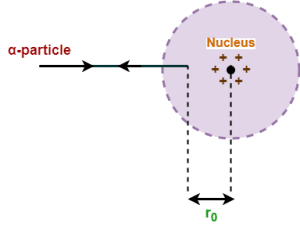
At this distance r₀, the entire initial kinetic energy of the α-particle gets converted into electrostatic potential energy of the system.

 

Thus, the distance of closest approach (r₀) may be defined as-

 

The distance of the charged particle from the center of the nucleus at which the entire initial kinetic energy of the charged particle gets converted into the electrostatic potential energy of the particle and the nucleus is called as distance of closest approach.

 

Expression for Distance of Closest Approach-

 

Applying the law of conservation of mechanical energy, we have-

 

 

Estimation of Nuclear Size-

 

• The α-particle scattering experiment provides an important way to determine an upper limit on the size of the nucleus.
• The size of the nucleus can be estimated by obtaining the point of closest approach of the α-particle.
• Since the α-particle can not touch the boundary of the nucleus due to strong repulsion, so the radius of the nucleus must be smaller than distance of closest approach (r₀).
• In other words, the maximum possible radius of the nucleus can be r₀.

 

 

Read the next article on-

Impact Parameter

 

Get more notes & other study material of the Chapter Atoms.