Speed of Electron in Nth Bohr Orbit

Speed of Electron in N^th Bohr Orbit-

 

Before you go through this article, make sure that you have gone through the previous article on Bohr’s Atomic Model.

 

We have learnt that-

• Electrons revolve around the nucleus in fixed energy orbits called as stationary states.
• Of all the possible circular orbits, an electron revolves only in those circular orbits in which its angular momentum is an integral multiple of h/2π.

 

In this article, we will derive the expression for the speed of electron in n^th Bohr orbit.

 

Deriving Expression For The Speed of Electron in N^th Bohr Orbit-

 

Consider a single electron species having atomic number Z. It consists of a nucleus with a charge +Ze and a single electron of charge -e which revolves around it in a circular orbit of radius R with a speed v.

 

 

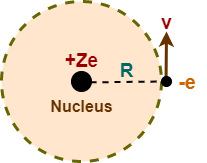
To keep the electron in its orbit, the centripetal force on this electron must be equal to the electrostatic force of attraction between the nucleus and the electron. So, we must have-

 

 

By Bohr’s quantization condition of angular momentum, we know-

 

 

From equations (1) and (2), we have-

 

This is the required expression for the speed of electron in n^th Bohr orbit.

 

Kindly note that here c denotes the speed of light in vacuum (3 x 10⁸ m/s).

 

Also Read- Radius of N^th Bohr Orbit

 

On substituting the values of known constants in the above expression, we get-

 

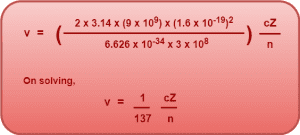
This is the simplified expression for the speed of electron in n^th Bohr orbit.

 

Kindly note that the value of fine structure constant (α) is 1/137 and it is a unit less and a dimensionless constant.

 

Important Note It is important to note that the speed of electron in the permitted orbits varies inversely with n.

 

Read the next article on-

Energy of Electron in N^th Bohr Orbit

 

Get more notes & other study material of the Chapter Atoms.