Electric Charge-

 

Before you go through this article, make sure that you have gone through the previous article on Electric Charge. It explains the basic concepts related to electric charge.

 

We have learnt-

• Two like point charges repel each other.
• Two unlike point charges attract each other.

 

In this article, we will discuss about Coulomb’s Law.

 

Coulomb’s law helps us to calculate the magnitude of Electric Force between two stationary point charges.

 

Coulomb’s Law-

 

The French physicist Charles Augustine de Coulomb experimentally measured the electric forces between small charged spheres by using a torsion balance.

He formulated his observations in the form of Coulomb’s law.

 

Coulomb’s law states that- The magnitude of force of attraction or repulsion between two stationary point charges is- directly proportional to the product of the magnitude of the two charges inversely proportional to the square of the distance between them.

 

Let two point charges q₁ and q₂ are at rest and separated by a distance r, then they exert a force on each other called electrostatic force.

According to Coulomb’s law, the force F between the two charges is such that-

On combining, we get-

Or

(Equation-01)

 

Here, k is a constant of proportionality called as electrostatic force constant or Coulomb’s constant.

 

Coulomb’s Constant-

 

The value of Coulomb’s constant depends upon the following two factors-

• the system of unit chosen to measure F, q₁, q₂ and r
• the nature of medium between the two charges

 

In SI unit,

(Equation-02)

 

Here,

• ε = absolute electrical permittivity of the medium present between the two charges
• ε₀ = absolute electrical permittivity of the free space
• ε_r = relative electrical permittivity of the medium present between the two charges also called as dielectric constant.

 

What is permittivity? Permittivity is a property of the medium which determines the electric force between two charges present in that medium.

 

Using equation-02 in equation-01, we get-

(Equation-03)

 

Dielectric Constant-

 

• The dielectric constant of a material medium can be defined as the ratio of the absolute electrical permittivity of the medium to the absolute electrical permittivity of the free space.
• It is denoted by K.
• It expresses the extent to which a material can hold electric flux in it.

 

Mathematically,

 

 

As it is the ratio of two like entities, it is a unit less and dimensionless quantity. It is a pure number.

 

The following table lists the value of dielectric constant for different materials-

 

Medium	Value of Dielectric Constant
Air / Vacuum	1
Metals	Infinite
Water	80

 

For free space i.e. air or vacuum, ε_r = 1. Hence, equation-03 becomes-

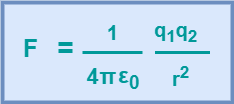
(Equation-04)

 

Absolute Electrical Permittivity of Free Space (ε₀)-

 

The value of absolute electrical permittivity of free space (ε₀) is given as-

 

Deriving SI unit of ε₀–

 

From equation-04, we have-

 

We know, in SI,

• The unit of q₁ and q₂ (charges) is coulomb (C)
• The unit of F (force) is newton (N)
• The unit of r (distance) is meter (m)

 

So, the SI unit of ε₀ may be calculated as-

 

Deriving Dimensional Formula of ε₀–

 

From equation-04, we have-

 

We know,

• The dimensional formula of q₁ or q₂ is [AT]
• The dimensional formula of F is [MLT^-2]
• The dimensional formula of r is [L]

 

Now, the dimensional formula of ε₀ can be given as-

[ε₀] = { [AT] x [AT] } / { [MLT^-2] x [L]² }

[ε₀] = [A²T²] / [ML³T^-2]

[ε₀] = [M^-1L^-3T⁴A²]

 

Thus,

The dimensional formula of ε0 is [M-1L-3T4A2].

 

Limitations of Coulomb’s Law-

 

The Coulomb’s law suffers from the following limitations-

• Coulomb’s law is valid only for stationary point charges.
• It is not a universal law.
• It loses its validity for distances less than 10^-15 m.
• It is difficult to implement Coulomb’s law where charges are in arbitrary shape.

 

Read the next article on-

Coulomb’s Law In Vector Form

 

Get more notes & other study material of the Chapter Electric Charges & Field.