Electric Field Due To An Electric Dipole

Electric Dipole-

 

Before you go through this article, make sure that you have gone through the previous article on Electric Dipole.

 

We have learnt-

• A system of two equal and opposite charges separated by a small distance is called as electric dipole.
• Electric dipole moment of an electric dipole is defined as the product of magnitude of either charge and the dipole length having its direction from -q to +q.

 

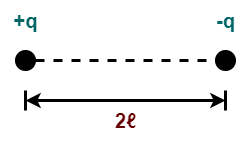
Electric Dipole

 

In this article, we will discuss Electric field due to an Electric dipole.

 

Electric Field Due To An Electric Dipole-

 

The electric field produced by an electric dipole is called the electric field of electric dipole.

 

We will calculate the electric field due to an electric dipole at axial and equatorial positions.

 

Axial Position-

 

• The line joining the centers of two charges of the electric dipole and extended on either side is called as axial line of an electric dipole.
• Any point lying on the axial line is called as axial position or end-on position.

 

Equatorial Position-

 

• The line passing through the center of electric dipole and perpendicular to its length is called as equatorial line of an electric dipole.
• Any point lying on the equatorial line is called as equatorial position or broadside-on position.

 

 

Electric Field Due To Electric Dipole At An Axial Position-

 

Consider-

• An electric dipole consisting of two charges -q and +q separated by a distance of 2ℓ.
• We wish to find the electric field due to this dipole at an axial point P located at distance r from the center of electric dipole.

 

 

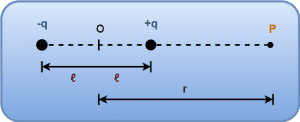
At point P,

• The electric field due to charge -q is towards -q (say E₁).
• The electric field due to charge +q is away from +q (say E₂).

 

This is shown in the following diagram-

 

 

Now, the electric field at point P due to charge -q is given by-

 

 

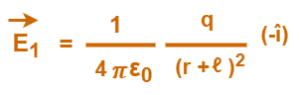
Similarly, the electric field at point P due to charge +q is given by-

 

 

By superposition principle, the net electric field at point P can be calculated now by taking the vector sum of electric fields due to each charge.

 

The net electric field at point P is given by-

 

 

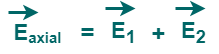
Substituting the values and solving, we have-

 

 

Thus, electric field due to electric dipole at an axial position is given by-

 

 

Important From here, we conclude that- The direction of electric field due to electric dipole at an axial position is always same as the direction of electric dipole moment. The angle between electric field at axial position and electric dipole moment is always 0o.

 

Special Case- For a Short Dipole

 

An electric dipole is said to be short if the distance of observation point from the center of dipole is much greater than dipole length i.e. r >> ℓ.

 

In this case,

r² – ℓ² ≈ r²

 

Thus, the above general formula for a short electric dipole reduces as-

 

 

Thus, electric field due to a short dipole at an axial position is-

• directly proportional to the electric dipole moment (p) of the electric dipole
• inversely proportional to the cube of the distance of observation point from the center of electric dipole.

 

Electric Field Due To Electric Dipole At An Equatorial Position-

 

Consider-

• An electric dipole consisting of two charges -q and +q separated by a distance of 2ℓ.
• We wish to find the electric field due to this dipole at an equatorial point P located at distance r from the center of electric dipole.

 

 

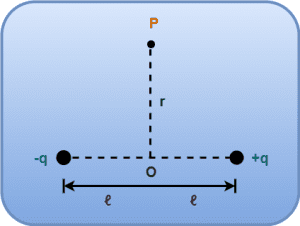
At point P,

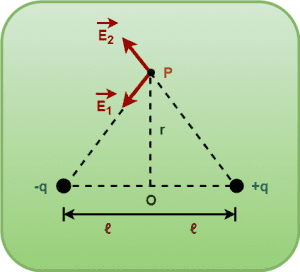
• The electric field due to charge -q is towards -q (say E₁).
• The electric field due to charge +q is away from +q (say E₂).

 

This is shown in the following diagram-

 

 

Let the line joining the two charges of electric dipole with the observation point P makes an angle θ with the dipole length.

Then using geometry, we have-

 

 

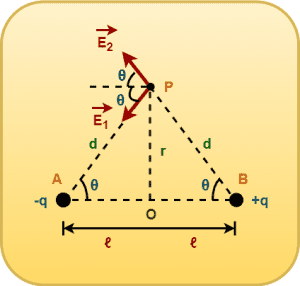
Using Pythagoras theorem,

d² = r² + ℓ²

 

The magnitude of electric field at point P due to both the charges -q and +q would be same.

 

Now, the magnitude of electric field at point P due to charges -q and +q is given by-

 

 

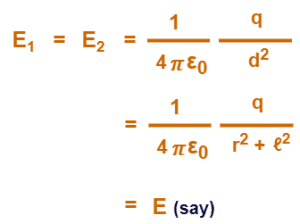
By superposition principle, the net electric field at point P can be calculated now by taking the vector sum of electric fields due to each charge.

 

The net electric field at point P is given by-

 

 

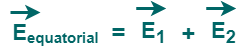
The magnitude of net electric field at point P (equatorial position) can be calculated as-

 

 

Direction of Electric Field-

 

Since the magnitude of E₁ and E₂ is same, so the direction of net electric field passes through the angle bisector of the angle (2θ) between the two electric field vectors as shown-

 

 

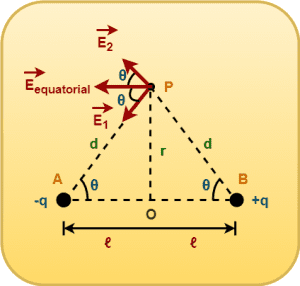
Clearly, the direction of net electric field at equatorial position is opposite to the direction of electric dipole moment.

 

Thus, electric field due to electric dipole at an equatorial position is given by-

 

 

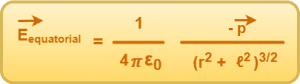
Important From here, we conclude that- The direction of electric field due to electric dipole at an equatorial position is always opposite to the direction of electric dipole moment. The angle between electric field at equatorial position and electric dipole moment is always 180o.

 

Special Case- For a Short Dipole

 

An electric dipole is said to be short if the distance of observation point from the center of dipole is much greater than dipole length i.e. r >> ℓ.

 

In this case,

r² + ℓ² ≈ r²

 

Thus, the above general formula for a short electric dipole reduces as-

 

 

Thus, electric field due to a short dipole at an equatorial position is-

• directly proportional to the electric dipole moment (p) of the electric dipole
• inversely proportional to the cube of the distance of observation point from the center of electric dipole.

 

Important Relation-

 

From the above discussion, the relation between magnitude of electric field at axial and equatorial position for a short electric dipole is-

 

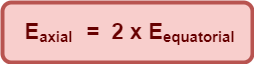
(Important)

 

Read the next article on-

Electric Dipole In Uniform Electric Field

 

Get more notes & other study material of the Chapter Electric Charges & Field.