Electric Field Due To Thin Spherical Shell

Gauss’s Law-

 

Before you go through this article, make sure that you have gone through the previous article on Gauss’s Law.

 

We have learnt-

• Gauss’s Law helps to find the total electric flux through any closed surface.
• It states that the total electric flux through any closed surface is 1/ε_o times the net charge enclosed within it.

 

Applications of Gauss’s Law-

 

Using Gauss’s law, we will calculate the electric field due to a-

• thin infinite long line charge
• uniformly charged infinite plane sheet
• uniformly charged thin spherical shell

 

In this article, we will discuss the electric field due to a thin spherical shell.

 

Electric Field Due To A Charged Thin Spherical Shell-

 

Consider a positive charge Q uniformly distributed on the surface of a spherical shell of radius R.

Direction of Electric Field-

 

The electric field due charged spherical shell is directed-

• radially outwards if the shell contains a positive charge
• radially inwards if the shell contains a negative charge

 

Magnitude of Electric Field-

 

By symmetry, the magnitude of electric field intensity is same at all points equidistant from the center of spherical shell.

 

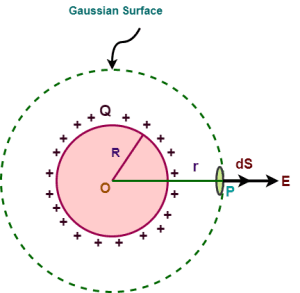
To calculate the magnitude of electric field intensity E at a point P located at a distance r from the center O of spherical shell using Gauss’s law, we consider an imaginary sphere of radius r with center O as the Gaussian surface.

 

A spherical Gaussian surface is an ideal choice because-

• At every point on the surface of sphere, the magnitude of electric field intensity is constant.
• The angle between electric field intensity and area vector at any point on the Gaussian surface will be 0°.

 

There are following three cases possible-

1. When observation point lies outside the shell i.e. r > R
2. When observation point lies on the surface of shell i.e. r = R
3. When observation point lies inside the shell i.e. r < R

 

Case-01: When observation point lies outside the shell (r>R)

 

We draw a spherical Gaussian surface of radius r (>R) with O as the center as shown-

 

 

 

This formula resembles the Electric Field due to a Point Charge.

 

Important Note Electric field intensity due to a charged spherical shell at a point outside the shell is such as if the entire charge were concentrated at the center of the sphere.

 

Case-02: When observation point lies on the surface of the shell (r=R)

 

We draw a spherical Gaussian surface of radius r=R with O as the center as shown-

 

 

Important Note Electric field intensity due to a charged spherical shell at any point on its surface is maximum.

 

Case-03: When observation point lies inside the shell (r<R)

 

We draw a spherical Gaussian surface of radius r (<R) with O as the center as shown-

 

 

 

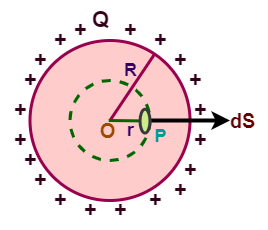
Important Note Electric field intensity due to a charged spherical shell at any point inside the shell is zero.

 

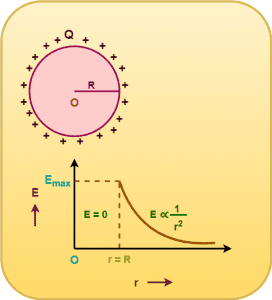
Based on the above discussion, the electric field due to charged thin spherical shell can be summarized as-

 

 

It is again worth noticing that due to a charged thin spherical shell-

• The electric field intensity at any point inside the shell is zero.
• The electric field intensity is maximum at the surface of shell.
• The electric field intensity then decreases and becomes zero at infinity.

 

Graph-

 

The following graph shows the variation of electric field intensity due to a charged thin spherical shell with distance from its center-

 

 

Also Check-

• Electric field due to a thin Infinite long line charge
• Electric field due to a thin infinite plane sheet of charge

 

Get more notes & other study material of the Chapter Electric Charges & Field.