Electric Flux-

 

Before you go through this article, make sure that you have gone through the previous article on Electric Flux.

 

We have learnt-

• Electric flux is a measure of the total number of electric field lines passing perpendicularly through a given area.
• It is denoted by Φ and given by the formula Φ = EAcosθ.
• Its SI unit is NC^-1m².

 

In this article, we will learn about Gauss’s Law.

 

Gauss’s Law-

 

Gauss’s Law gives a relationship between the total electric flux passing through any closed surface and the net electric charge enclosed within the surface.

 

It states that-

 

The surface integral of the electric field intensity over any closed hypothetical surface (called as Gaussian surface) in free space is equal to 1/εo times the total electric charge enclosed within the surface. OR The total electric flux through a closed surface is 1/εo times the total electric charge enclosed within the surface.

 

Mathematically, it can be expressed as-

 

 

Special Cases-

 

It is important to note the following special cases regarding Gauss’s law-

 

Case-01: If the closed surface does not enclose any charge-

 

• In this case, the charge enclosed by the Gaussian surface is zero i.e. q_enc = 0. So, Φ_net = 0.
• Thus, the electric flux through a closed surface containing no charge is zero.

 

Example-

Consider a Gaussian surface enclosing no electric charge as shown-

 

 

Since the charge enclosed inside the Gaussian surface is zero, so the electric flux through it will also be zero.

 

Case-02: If the closed surface contains two equal & opposite charges-

 

• In this case, the net charge enclosed by the Gaussian surface becomes zero i.e. q_enc = 0. So, Φ_net = 0.
• The net flux is zero because inward electric flux due to negative charge cancels the outward electric flux due to positive charge.
• Thus, the net electric flux through a closed surface containing two equal and opposite charges is zero.

 

Example-

Consider a Gaussian surface enclosing an electric dipole as shown-

 

 

Here, the net charge enclosed by the Gaussian surface = 5 μC + (-5 μC) = 0. Thus, Φ_net = 0.

 

Case-03: If the closed surface has discrete distribution of charges-

 

In this case, the net charge enclosed by the surface is obtained by the algebraic sum of all the individual charges. Then, Φ_net = q_enc / ε_o.

 

Example-

Consider a Gaussian surface enclosing discrete charges as shown-

 

 

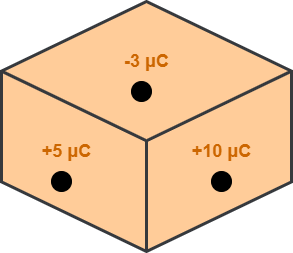
Here, the net charge enclosed by the Gaussian surface = 5 μC + 10 μC + (-3 μC) = +12 μC.

Thus, Φ_net = +12 μC / ε_o.

 

Case-04: Electric flux through a Gaussian surface is independent of its Shape-

 

The electric flux through a Gaussian surface does not depend on the shape of the Gaussian surface.

 

Example-

Consider a charge of +5 μC is enclosed by the Gaussian surfaces as shown-

 

 

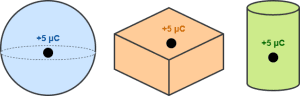
Here, each Gaussian surface has a different shape (spherical, cuboidal, cylinderical) but encloses the same charge. So, electric flux through each of them will be same.

 

Case-05: Electric flux through a Gaussian surface is independent of its Size-

 

The electric flux through a Gaussian surface does not depend on the size of the Gaussian surface.

 

Example-

Consider a charge of +5 μC is enclosed by the Gaussian surfaces as shown-

 

 

Here, each Gaussian surface has a different size but encloses the same charge. So, electric flux through each of them will be same.

 

Case-06: Electric flux through a Gaussian surface is independent of the position of Charge-

 

The electric flux through a Gaussian surface does not depend on the position of charge inside the Gaussian surface.

 

Example-

Consider a charge of +5 μC is enclosed by the Gaussian surfaces as shown-

 

 

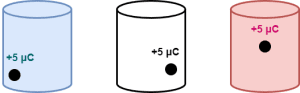
Here, the position of charge inside each Gaussian surface is different but each encloses the same charge. So, electric flux through each of them will be same.

 

Case-07: Net electric flux through a Gaussian Surface is proportional to the amount of Charge-

 

The electric flux through a Gaussian surface is directly proportional to the amount of electric charge enclosed within the surface.

 

Example-

Consider two identical Gaussian surfaces enclosing charges as shown-

 

 

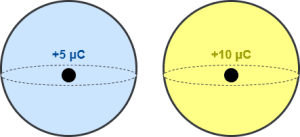
Here, the charge enclosed by the 2nd Gaussian surface is double. So, the electric flux through it will also be double of the electric flux through the 1st surface.

 

Case-08: If a Charge is present outside the Gaussian Surface-

 

• A charge present outside the Gaussian surface does not affect the net electric flux passing through the surface.
• This is because due to an outside charge, inward electric flux = outward electric flux .

 

 

Example-

Consider a charge of +5 μC is present outside the Gaussian surface as shown-

 

 

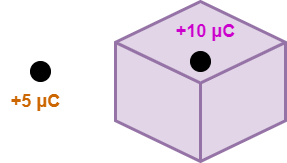
Here, the charge of +5 μC present outside the Gaussian surface does not affect the net electric flux through it. Here, q_enc = +10 μC, so Φ_net = +10 μC / ε_o.

 

Read the next article on-

Proof of Gauss’s Law

 

Get more notes & other study material of the Chapter Electric Charges & Field.