Deducing Coulomb’s Law From Gauss’s Law

Gauss’s Law-

 

Before you go through this article, make sure that you have gone through the previous article on Gauss’s Law.

 

We have learnt-

• Gauss’s Law helps to find the total electric flux through any closed surface.
• It states that the total electric flux through any closed surface is 1/ε_o times the net charge enclosed within it.

 

In this article, we will deduce Coulomb’s Law from Gauss’s Law.

 

Coulomb’s Law From Gauss’s Law-

 

Coulomb’s law and Gauss’s law are complementary to each other i.e. any of the two can be regarded as basic and then the other can be derived out of it.

 

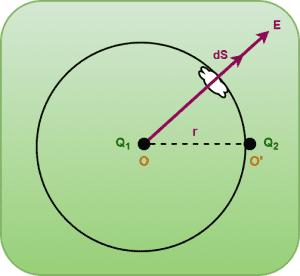
To derive Coulomb’s law from Gauss’s law, consider two point charges Q₁ and Q₂ separated by a distance r as shown-

 

 

We draw a spherical Gaussian surface of radius r with O as the center and calculate the electric field intensity on it using Gauss’s law.

 

 

According to Gauss’s theorem,

 

 

Clearly,

• The angle between electric field intensity and elemental area vector over the surface at any point = 0°
• The charge enclosed by the Gaussian surface, q_enc = Q₁

 

Substituting and solving, we have-

 

 

This is the value of electric field intensity at the position of charge Q₂.

Therefore, force experienced by charge Q₂ is given by-

 

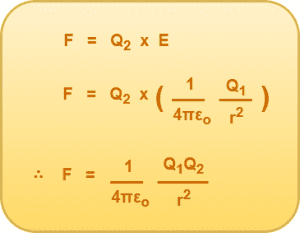
This is a mathematical form of Coulomb’s law.

 

Hence, Coulomb’s law is derived from Gauss’s law.

 

Read the next article on-

Charge Density & Its Types

 

Get more notes & other study material of the Chapter Electric Charges & Field.