Electric Field Due To Infinite Line Charge

Gauss’s Law-

 

Before you go through this article, make sure that you have gone through the previous article on Gauss’s Law.

 

We have learnt-

• Gauss’s Law helps to find the total electric flux through any closed surface.
• It states that the total electric flux through any closed surface is 1/ε_o times the net charge enclosed within it.

 

Applications of Gauss’s Law-

 

Using Gauss’s law, we can easily calculate the electric field due to a-

• thin infinite long line charge
• thin infinite plane sheet of charge
• uniformly charged thin spherical shell

 

In this article, we will discuss the electric field due to an infinite line charge.

 

Electric Field Due To A Thin Infinitely Long Line Charge-

 

Consider a thin infinitely long straight wire having a uniform linear charge density λ Cm^-1 as shown-

 

 

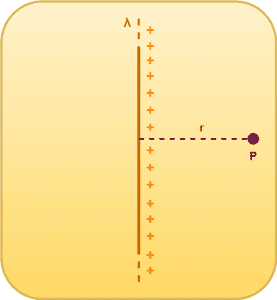
Direction of Electric Field-

 

By symmetry, the electric field due to a line charge is directed-

• perpendicularly outwards if the line charge carries a positive charge
• perpendicularly inwards if the line charge carries a negative charge

 

Magnitude of Electric Field-

 

By symmetry, the magnitude of electric field intensity is same at all points equidistant from the line charge.

 

To calculate the magnitude of electric field intensity E at a point P located at a distance r from the line charge using Gauss’s law, we consider an imaginary cylinder of radius r as the Gaussian surface.

 

A cylinderical Gaussian surface is an ideal choice because-

• At every point on the curved surface of cylinder, the magnitude of electric field intensity is constant.
• The electric flux passing through the circular faces of cylinder will be zero.

 

 

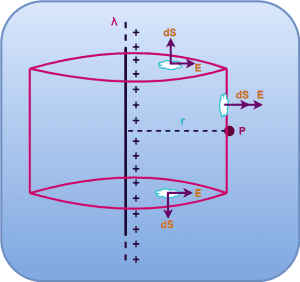
According to Gauss’s theorem, we have-

 

(Equation-01)

 

The cylinderical Gaussian surface can be divided into three parts-

1. Top circular face
2. Bottom circular face
3. Curved surface

 

Then, equation-01 can be written as-

 

 

In terms of Coulomb’s Constant, the above expression for electric field intensity can be rewritten as-

 

 

Graph-

 

Clearly, the electric field intensity due to an infinite line charge is inversely proportional to the distance of observation point from the line charge i.e.

 

 

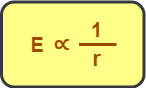
The graph showing the variation of electric field intensity due to an infinite line charge with distance from it is-

 

 

Also Check-

• Electric field due to a thin infinite plane sheet of charge
• Electric field due to a charged thin spherical shell

 

Read the next article on-

Electric Field Due To A Thin Infinite Plane Sheet Of Charge

 

Get more notes & other study material of the Chapter Electric Charges & Field.