Electrical Capacitance of A Conductor-

 

Before you go through this article, make sure that you have gone through the previous article on Electrical Capacitance of a Conductor.

 

We have learnt-

• The electrical capacitance of a conductor is a measure of its ability to store electric charge or energy.
• It depends on the shape and size of the conductor.
• Its SI unit is farad (F).

 

If charge Q raises the potential of conductor by V, then its electrical capacitance is given by the formula-

 

 

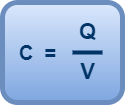
In this article, we will learn about the capacitance of an isolated spherical conductor.

 

Capacitance of An Isolated Spherical Conductor-

 

Consider an isolated spherical conductor of radius R in free space. Let a charge Q is given to the sphere which spreads uniformly on its surface.

 

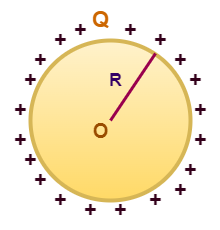
The electric potential at any point on the surface of sphere is given by-

 

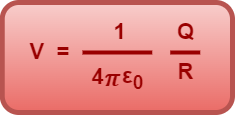
(Equation-01)

 

Also Read- Electric Potential Due To Uniformly Charged Thin Spherical Shell

 

Now, capacitance is given by the formula-

 

(Equation-02)

 

Using Equation-01 in Equation-02, we get-

 

 

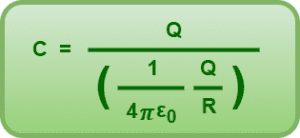
On solving, we get-

 

 

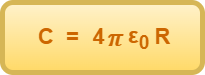
This is the required formula for the capacitance of an isolated spherical conductor.

 

Important Notes-

 

Note-01:

 

The capacitance of an isolated spherical conductor is directly proportional to its radius.

 

 

Thus, larger the sphere, larger is its capacitance & smaller the sphere, smaller is its capacitance.

 

Note-02:

 

The above formula for capacitance C= 4πε_oR is valid for both hollow and solid spherical conductors.

 

Read the next article on-

Introduction to Capacitor

 

Get more notes & other study material of the Chapter Electrostatic Potential & Capacitance.