Energy Stored In A Charged Capacitor-

 

• The process of charging a capacitor is equivalent to that of transferring charge from one plate to the other plate of the capacitor.
• At any stage of the charging, there exists a potential difference between the plates of the capacitor.
• Therefore, some work must be done to transfer charge from one plate to the other plate of the capacitor.
• This work is stored as electrostatic potential energy in the capacitor.

 

 

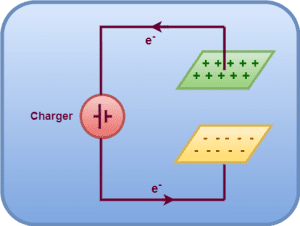
Deriving Formula For Energy Stored In Charged Capacitor-

 

Let at any instant, a charge q be on the capacitor. Then, potential difference between the plates of the capacitor is given by-

 

 

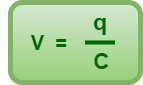
If extra charge dq is transferred to the capacitor, then work done to do so is given by-

 

 

If the final charge on the capacitor is Q, then the total work done is given by-

 

 

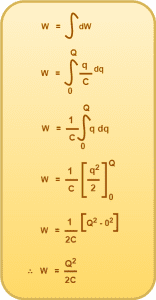
This work is stored as the electrostatic potential energy (U) of the capacitor. So, we have-

 

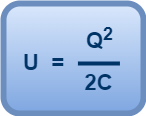
(Equation-01)

 

Other Expressions-

 

The above formula for energy stored in a charged capacitor can be expressed in the following two forms-

 

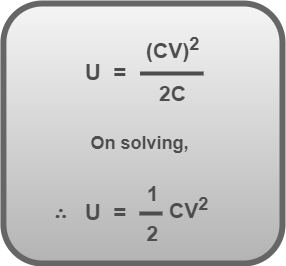
Substituting Q = CV in equation-01, we get-

 

 

Substituting C = Q/V in equation-01, we get-

 

 

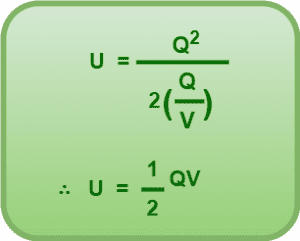
Thus, energy stored in a charged capacitor is given by the formulae-

 

 

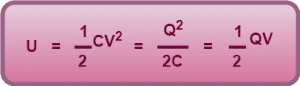
It is important to note that the electrostatic potential energy of a capacitor is stored in the form of electric field between the plates of the capacitor.

 

Electrostatic Energy Density-

 

Energy stored per unit volume of the space between the plates of the capacitor is called as energy density.

 

Consider a parallel plate capacitor having-

• Electrical capacitance = C
• Area of each plate = A
• Distance between the plates = d

 

When the capacitor is charged to voltage V, the energy stored in the capacitor is given by-

 

(Equation-01)

 

But capacitance of a parallel plate capacitor is given by-

 

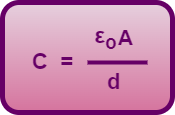
(Equation-02)

 

If E is the electric field between the plates, then potential difference V across the plates is given by-

 

(Equation-03)

 

Using Equations-02 and 03 in Equation-01, we get-

 

 

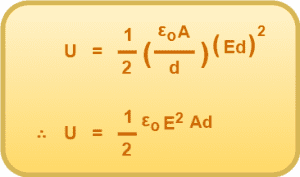
Since volume of the capacitor = Ad. Thus,

 

 

• The SI unit of energy density is J m^-3.
• The dimensional formula of energy density is [ML^-1T^-2].

 

Get more notes & other study material of the Chapter Electrostatic Potential & Capacitance.