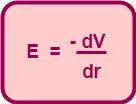Relation Between Electric Field & Potential

Electric Potential-

 

Before you go through this article, make sure that you have gone through the previous article on Work Done In Moving Charge In Electric Field.

 

We have learnt-

• An external agent has to do some work against the electrostatic forces while moving a charge in an external electric field.
• The work done by an external agent in moving a charge q_o from initial point ‘i’ to final point ‘f’ in an electric field is given by the formula-

 

 

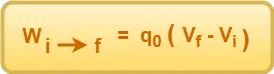
In this article, we will learn the Relation Between Electric Field & Electric Potential.

 

Relation Between Electric Field & Electric Potential-

 

Consider-

• A positive point charge Q is fixed at a point.
• We wish to find the relation between electric field and electric potential.
• Another point charge q_o is being moved by an external agent from point A to point B in the electric field of source charge Q.

 

 

Consider at any instant, the charge q_o is present at some point P at a distance r from the source charge Q during its motion from A to B.

 

 

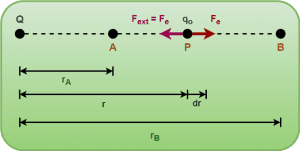
The work done by external agent in causing a small displacement dr from point P is given by-

 

(Equation-01)

 

To calculate the total work done by the external agent in taking the charge q_o from point A to point B, we integrate the above calculated small work done dW in Equation-01 as-

 

 

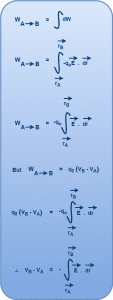
Thus, the relation between electric field and electric potential is given as-

 

(Very Important)

 

Special Scenario-

 

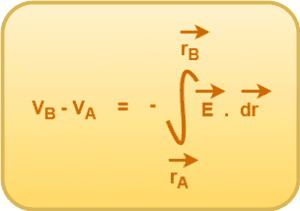
If the electric field in a region is everywhere uniform, then the above general relation between electric field and electric potential can be written as-

 

 

Thus, in a region of uniform electric field, on moving from point A to point B, the change in electric potential is given by-

 

(Very Important)

 

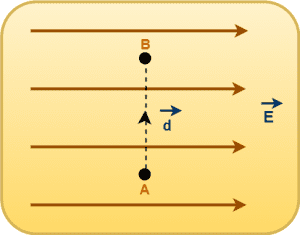
Special Cases-

 

Case-01: When θ = 0°

 

On moving in the direction of electric field, the angle between electric field & displacement vector is 0°.

 

 

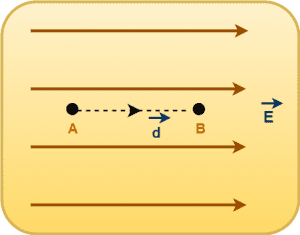
We have-

V_B – V_A = -Edcos0°

V_B – V_A = -Ed(1)

∴ V_B – V_A = -Ed

 

This shows that-

• On moving in the direction of electric field, the electric potential decreases.
• On moving a distance d, the electric potential decreases by the amount Ed.

 

Case-02: When θ = 180°

 

On moving in the opposite direction of electric field, the angle between electric field & displacement vector is 180°.

 

 

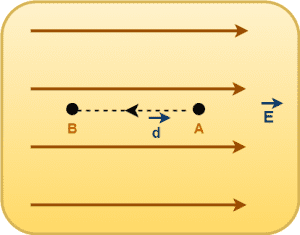
We have-

V_B – V_A = -Edcos180°

V_B – V_A = -Ed(-1)

∴ V_B – V_A = Ed

 

This shows that-

• On moving in the opposite direction of electric field, the electric potential increases.
• On moving a distance d, the electric potential increases by the amount Ed.

 

Case-03: When θ = 90°

 

On moving perpendicular to the direction of electric field, the angle between electric field & displacement vector is 90°.

 

 

We have-

V_B – V_A = -Edcos90°

V_B – V_A = -Ed(0)

∴ V_B – V_A = 0

Or V_B = V_A

 

This shows that-

• On moving perpendicular to the direction of electric field, the electric potential remains constant.
• This gives rise to the concept of Equipotential Surface.

 

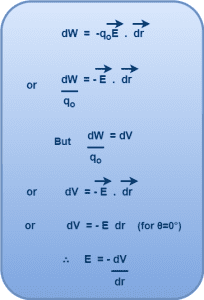
Another Important Relation E = -dV/dr   From Equation-01, we have-   From here, we conclude that- Electric Field is the negative of potential gradient which can be mathematically expressed as-     Here, negative sign shows that electric potential decreases in the direction of electric field.

 

Read the next article on-

Electric Potential Due To Thin Infinitely Long Line Charge

 

Get more notes & other study material of the Chapter Electrostatic Potential & Capacitance.