Parallel Plate Capacitor-

 

Before you go through this article, make sure that you have gone through the previous article on Parallel Plate Capacitor.

 

We have learnt-

• A parallel plate capacitor is an arrangement of two equally & oppositely charged plates of equal area separated by a certain distance through a dielectric.
• The capacitance of an air filled parallel plate capacitor is given by-

 

 

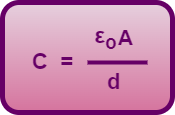
• The capacitance of a parallel plate capacitor completely filled with a dielectric is given by-

 

 

• The capacitance of an air filled parallel plate capacitor increases to K times when a dielectric having dielectric constant K is filled between its plates.

 

 

In this article, we will learn about the parallel plate capacitor partially filled with a dielectric.

 

Capacitance of Parallel Plate Capacitor Partially Filled With Dielectric-

 

Let us consider a parallel plate capacitor having-

• Q = Magnitude of charge on each plate
• A = Area of each plate
• d = distance between its two plates
• a dielectric having dielectric constant K and thickness t (t < d) between its two plates

 

 

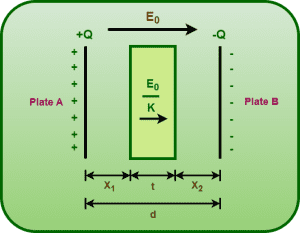
Now, we wish to find the capacitance of a parallel plate capacitor partially filled with a dielectric.

 

Step-01: Calculating the Potential difference Across Capacitor (V)-

 

We know,

• A uniform electric field exists between the two plates of capacitor.
• If σ is the surface charge density of each plate, then electric field between the two plates (in free space) is given by-

 

 

• Then, the electric field inside the dielectric placed in the electric field E_o is given by-

 

 

Let V_A = Electric potential of plate A and V_B = Electric potential of plate B.

To calculate the potential difference across the capacitor, we find the potential difference between its two plates i.e. V_A – V_B.

 

We travel from plate A to plate B and write the changes in electric potential. Then, we have-

 

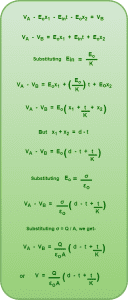
(Equation-02)

 

Step-02: Calculating the Capacitance of Capacitor (C)-

 

We know, the capacitance of a capacitor is given by the formula-

 

 

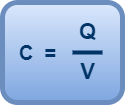
Substituting equation-02, we get-

 

 

Thus, the capacitance of a parallel plate capacitor partially filled with a dielectric is given by the formula-

 

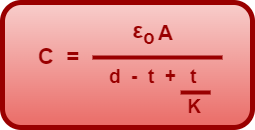
OR

 

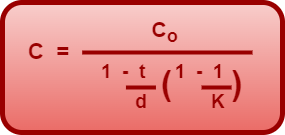
Special Case-

 

If the dielectric is completely filled between the two plates of the capacitor, then t = d.

Substituting t = d in the above formula, we get-

 

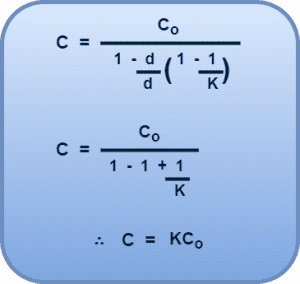
We derived the same formula in the previous article also.

 

Read the next article on-

Series Combination of Capacitors

 

Get more notes & other study material of the Chapter Electrostatic Potential & Capacitance.