Equipotential Surface-
Before you go through this article, make sure that you have gone through the previous article on Equipotential Surface.
We have learnt-
- An equipotential surface is any surface at all points of which the electric potential remains constant.
- Work done in moving a test charge on an equipotential surface is always zero.
In this article, we will sketch the equipotential surfaces due to different charge configurations.
Sketching Equipotential Surfaces-
We use the following properties to sketch equipotential surfaces due to different charge configurations-
- An equipotential surface is always perpendicular to the electric field at every point.
- Two equipotential surfaces can never intersect each other.
- Equipotential surfaces are closer together in the regions of strong electric field and farther apart in the regions of weak electric field.
Here, we will sketch the equipotential surfaces for the following-
1. Due to an isolated point charge
2. Due to a uniform electric field
3. Due to a system of two equal and opposite charges
4. Due to a system of two equal positive charges
5. Due to an infinite long line charge
1. Due To An Isolated Point Charge-
For an isolated point charge, the equipotential surfaces are a family of concentric spheres around the point charge.
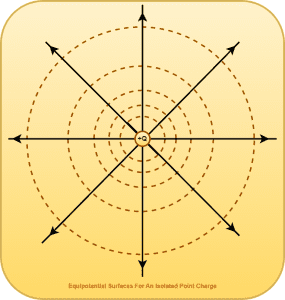
It may be noted that-
The equipotential surfaces due to any spherical charge are a family of concentric spheres around the charge.
2. Due To A Uniform Electric Field-
For uniform electric field, the equipotential surfaces are a family of planes perpendicular to the field lines.
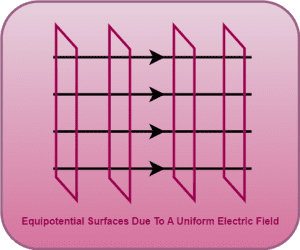
It may be noted that-
The same equipotential surfaces would be sketched due to an infinite plane sheet of charge as it creates a uniform electric field.
3. Due To A System Of Two Equal & Opposite Charges-
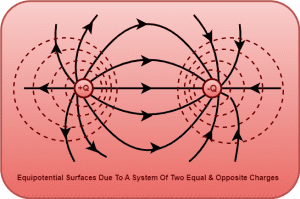
4. Due To A System Of Two Equal Positive Point Charges-
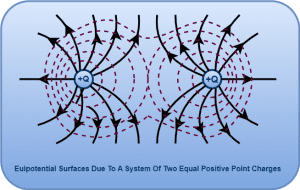
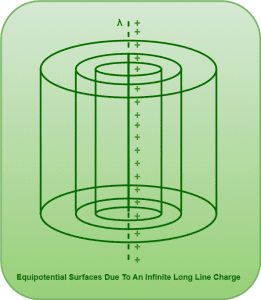
5. Due To An Infinite Long Line Charge-
Due to an infinite long line charge, equipotential surfaces are co-axial cylinders having their common axes at the line charge.
Read the next article on-
Electric Potential Energy of a System of Point Charges
Get more notes & other study material of the Chapter Electrostatic Potential & Capacitance.

