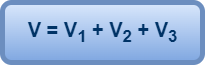Combination of Capacitors-

 

Capacitors may be connected to each other in the following ways-

 

 

1. Series Combination
2. Parallel Combination
3. Mixed Combination

 

In this article, we will discuss series combination of capacitors.

 

Series Combination of Capacitors-

 

Two or more capacitors are said to be connected in series combination if- the negative plate of the first capacitor is connected to the positive plate of the second and the negative plate of the second to the positive of third and so on such that the magnitude of charge on each capacitor is same when connected to a cell or battery

 

Expression For Equivalent Capacitance-

 

Consider-

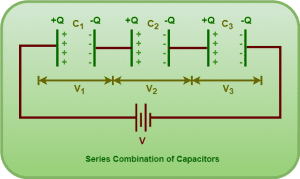
• Three capacitors of capacitances C₁, C₂ and C₃ are connected in series across a battery.
• The battery maintains a potential difference V across the combination.

 

In series combination, the charge on each capacitor is same but the potential difference divides among the individual capacitors.

 

 

In series combination, the potential difference across the combination is equal to the sum of potential difference across the individual capacitors i.e.

 

(Equation-01)

 

In steady state, the charge on each capacitor is same and given by-

• For 1^st capacitor, Q = C₁V₁
• For 2^nd capacitor, Q = C₂V₂
• For 3^rd capacitor, Q = C₃V₃

 

From here, we have-

 

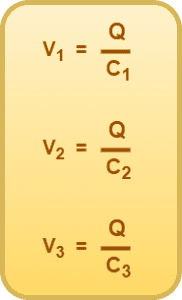
Using these in Equation-01, we get-

 

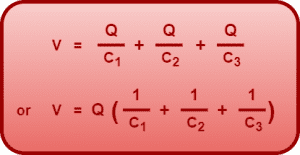
(Equation-02)

 

Now, we wish to replace the above series combination of capacitors with a single equivalent capacitor.

 

An equivalent capacitor is one which draws the same charge from the battery as drawn by the individual capacitors altogether.

 

Replacing the series combination with an equivalent capacitor, we have-

 

 

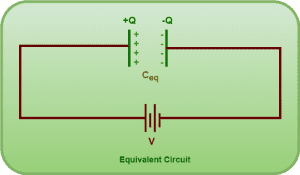
In steady state, for equivalent capacitor, we have Q = C_eqV.

 

From here, we have-

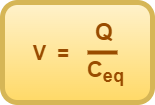
(Equation-03)

 

On comparing Equation-02 and Equation-03, we get-

 

 

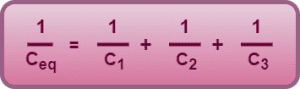
This is the required expression for equivalent capacitance for a series combination of capacitors.

The formula can be extended for n capacitors in the same way.

 

In series combination, the reciprocal of equivalent capacitance is equal to the sum of reciprocals of the individual capacitances.

 

Important Notes-

 

Note-01:

 

In series combination,

• The charge on each capacitor is same but potential difference divides among the individual capacitors.
• The potential difference across the combination is equal to the sum of potential difference across the individual capacitors.

 

Note-02:

 

If two capacitors having capacitances C₁ and C₂ are connected in series combination, then their equivalent capacitance is given by-

 

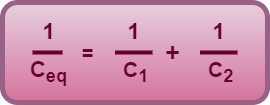
(Not Recommended to Use)

 

Taking LCM and then reciprocal, this formula for two capacitors can be rewritten as-

 

(Recommended to Use)

 

Trick To Learn Equivalent Capacitance = Product of two capacitors / Sum of two capacitors

 

If the capacitance of one capacitor is n times the capacitance of the other capacitor i.e. C₂ = nC₁ (say), then substituting in the above formula and solving, the formula can be rewritten as-

 

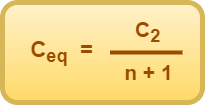
(Recommended to Use)

 

Trick To Learn Equivalent Capacitance = Big One / (n+1)

 

Note-03:

 

If n capacitors each of capacitance C are connected in series combination, then their equivalent capacitance is given by-

 

 

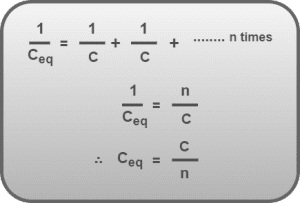
Note-04:

 

In series combination, the equivalent capacitance is smaller than the smallest individual capacitance.

 

Read the next article on-

Parallel Combination of Capacitors

 

Get more notes & other study material of the Chapter Electrostatic Potential & Capacitance.