Electric Potential Energy | Point Charges

Work Done In Moving A Charge In An Electric Field-

 

Before you go through this article, make sure that you have gone through the previous article on Work Done In Moving Charge.

 

We have learnt-

• An external agent needs to do some work in moving a charge in an external electric field.
• The work done in moving a charge q_o in an electric field from initial point ‘i’ to final point ‘f’ is given by-

 

 

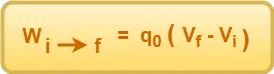
In this article, we will discuss about the electric potential energy of a system of point charges.

 

Electric Potential Energy of a System of Point Charges-

 

It is the energy possessed by a system of charges by virtue of their positions.

 

The electric potential energy of a system of point charges is defined as the amount of work done in assembling the charges at their respective locations by bringing them in from infinity.

 

Electric Potential Energy of a System of Two Point Charges-

 

Consider a system of two point charges as shown-

 

 

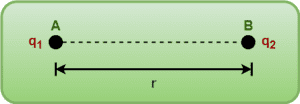
To calculate the electric potential energy of this system, we bring each of these from infinity one by one and calculate the work done in the process.

 

Step-01:

 

• We bring charge q₁ from infinity to point A.
• It takes no work to bring the first charge because there is no field yet to work against.

∴ W₁ = 0

 

Step-02:

 

• Now, we bring charge q₂ from infinity to point B.
• The work done in bringing charge q₂ from infinity to point B is given by-

 

 

The total work done in forming a two-charge system is given by-

 

 

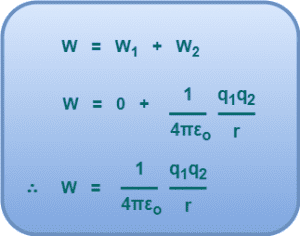
This work is stored in the form of electric potential energy of the system of two charges.

 

Thus, the electric potential energy of a system of two charges is given by-

 

Electric Potential Energy of a System of Three Point Charges-

 

Consider a system of three point charges as shown-

 

 

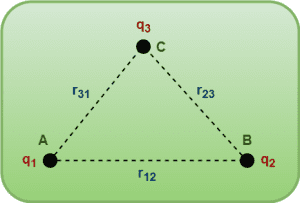
To calculate the electric potential energy of this system, we bring each of these from infinity one by one and calculate the work done in the process.

 

Step-01:

 

• We bring charge q₁ from infinity to point A.
• It takes no work to bring the first charge because there is no field yet to work against.

∴ W₁ = 0

 

Step-02:

 

• Now, we bring charge q₂ from infinity to point B.
• The work done in bringing charge q₂ from infinity to point B is given by-

 

 

Step-03:

 

• Now, we bring charge q₃ from infinity to point C.
• The work done in bringing charge q₃ from infinity to point C is given by-

 

 

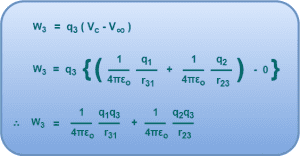
The total work done in forming a three-charge system is given by-

 

 

This work is stored in the form of electric potential energy of the system of three charges.

 

Thus, the electric potential energy of a system of three charges is given by-

 

Important Notes-

 

Note-01:

 

For two like charges,

• The potential energy of two like charges is positive.
• As the electrostatic force is repulsive, so a positive amount of work has to be done against this force to bring the charges from infinity to a finite separation.

 

For two unlike charges,

• The potential energy of two unlike charges is negative.
• As the electrostatic force is attractive, so a negative amount of work has to be done against this force to bring the charges from infinity to a finite separation.

 

Note-02:

 

While calculating the electric potential energy for a given system of charges using the above derived formulae, always put the value of charges with their proper signs.

 

Note-03:

 

To write the formula for electric potential energy of a system of any given number of charges,

• Just count the number of different pairs of charges (Number of pairs = ⁿC₂)
• Write the electric potential energy for each pair of charge
• Add the electric potential energy for each pair

 

Note-04:

 

Work done in dissociating a system of given charges is negative of the electric potential energy of the system of charges.

 

Read the next article on-

Potential Energy of Electric Dipole in Electric Field

 

Get more notes & other study material of the Chapter Electrostatic Potential & Capacitance.