Electric Potential Due To Electric Dipole

Electric Dipole-

 

Before you go through this article, make sure that you have gone through the previous article on Electric Dipole.

 

We have learnt-

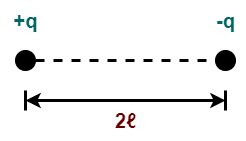
• A system of two equal and opposite charges separated by a small distance is called as electric dipole.
• We derived the expressions for Electric field due to an Electric dipole at axial and equatorial positions.

 

Electric Dipole

 

In this article, we will discuss Electric Potential due to an Electric dipole.

 

Electric Potential Due To An Electric Dipole-

 

We will calculate the electric potential due to an electric dipole at axial and equatorial positions.

 

Axial Position-

 

• The line joining the centers of two charges of the electric dipole and extended on either side is called as axial line of an electric dipole.
• Any point lying on the axial line is called as axial position or end-on position.

 

Equatorial Position-

 

• The line passing through the center of electric dipole and perpendicular to its length is called as equatorial line of an electric dipole.
• Any point lying on the equatorial line is called as equatorial position or broadside-on position.

 

 

Electric Potential Due To Electric Dipole At An Axial Position-

 

Consider-

• An electric dipole consisting of two charges -q and +q separated by a distance of 2ℓ.
• We wish to find the electric potential due to this dipole at an axial point P located at distance r from the center of electric dipole.

 

 

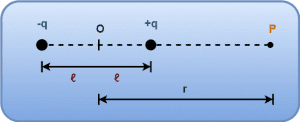
The electric potential at point P due to charge -q is given by-

 

 

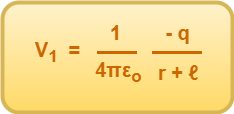
Also Read- Electric Potential Due To A Point Charge

 

Similarly, the electric potential at point P due to charge +q is given by-

 

 

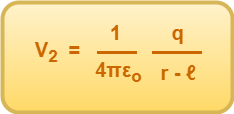
By superposition principle, the net electric potential at point P can be calculated now by taking the algebraic sum of electric potentials due to each charge.

 

The net electric potential at point P is given by-

 

 

Special Case- For a Short Dipole

 

An electric dipole is said to be short if the distance of observation point from the center of dipole is much greater than dipole length i.e. r >> ℓ.

 

In this case,

r² – ℓ² ≈ r²

 

Thus, the above general formula for a short electric dipole reduces as-

 

 

Thus, electric potential due to a short electric dipole at an axial position is-

• directly proportional to the electric dipole moment (p) of the electric dipole.
• inversely proportional to the square of the distance of observation point from the center of electric dipole.

 

Electric Potential Due To Electric Dipole At An Equatorial Position-

 

Consider-

• An electric dipole consisting of two charges -q and +q separated by a distance of 2ℓ.
• We wish to find the electric potential due to this dipole at an equatorial point P located at distance r from the center of electric dipole.

 

 

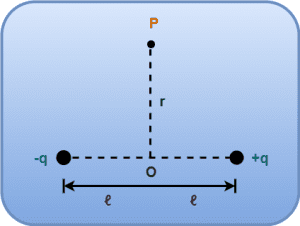
The electric potential at point P due to charge -q is given by-

 

 

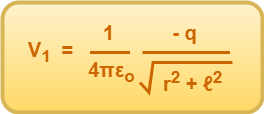
Similarly, the electric potential at point P due to charge +q is given by-

 

 

By superposition principle, the net electric potential at point P can be calculated now by taking the algebraic sum of electric potentials due to each charge.

 

The net electric potential at point P is given by-

 

 

Important Note Electric potential due to an electric dipole at an equatorial position is zero.

 

Read the next article on-

Work Done In Moving A Charge In Electric Field

 

Get more notes & other study material of the Chapter Electrostatic Potential & Capacitance.