Electric Potential | Infinite Line Charge

Electric Potential-

 

Before you go through this article, make sure that you have gone through the previous articles on-

• Electric Field Due To A Thin Infinitely Long Line Charge
• Relation Between Electric Field & Electric Potential

 

We have learnt-

The electric field due to a thin infinitely long line charge at a distance r from it is given by-

 

 

The relation between electric field and electric potential is given by-

 

 

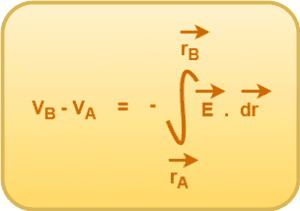
In this article, we will learn the electric potential due to a thin infinitely long line charge.

 

Electric Potential Due To A Thin Infinitely Long Line Charge-

 

Consider-

• A thin infinitely long straight wire having a uniform linear charge density λ Cm^-1.
• Two points A and B at perpendicular distances ‘a’ and ‘b’ respectively from the wire.

 

 

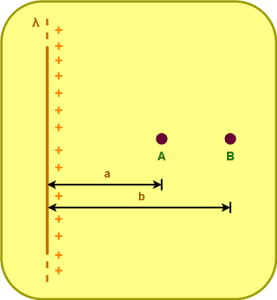
Let the electric potential at point A be V_A and the electric potential at point B be V_B.

We will travel from point A to point B and write the relation between electric field and electric potential.

 

Using the relation, we have-

 

 

Substituting the values we have-

 

 

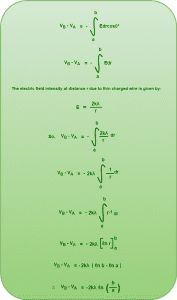
Here, negative sign represents that electric potential decreases in the direction of electric field.

 

Important Note In the above expression, We cannot find the value of electric potential at any one point by taking the other point at infinity. This would yield an absurd result of every point being at infinite potential. We could only find the potential difference between any two given points using the above derived result.

 

Read the next article on-

Electric Potential Due To Thin Infinite Plane Sheet of Charge

 

Get more notes & other study material of the Chapter Electrostatic Potential & Capacitance.