Electric Current-

 

Before you go through this article, make sure that you have gone through the previous articles on Electric Current & Drift Velocity.

 

We have learnt-

• Electric current is the flow of electric charges (free electrons) through a conductor in a preferred direction.
• Drift velocity is the average uniform velocity with which free electrons drift inside the conductor on the application of external electric field.

 

In this article, we will learn & derive-

• Relation Between Electric current & Drift velocity
• Relation Between Electric current & Relaxation time
• Ohm’s Law
• Relation Between Resistivity & Relaxation time

 

Relation Between Electric Current and Drift Velocity-

 

Consider a conductor with-

• Length of conductor = L
• Area of cross-section = A
• Number of free electrons per unit volume (free electron density) = n

 

 

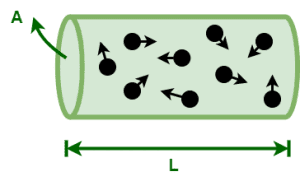
Then, total number of free electrons inside the conductor is given by-

N = Free electron density x Volume of the conductor

N = n x (A x L)

N = nAL

 

Total charge on free electrons inside the conductor,

Q = Total number of free electrons x Charge on one electron

Q = nAL x e

Q = nALe   ……………. (Equation-01)

 

Now, when a battery is connected across the two ends of the conductor, an electric field is set up inside the conductor across its two ends.

 

 

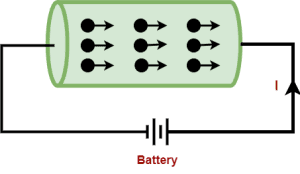
If the drift velocity of free electrons is v_d, then time taken by the electrons to cross the length of the conductor is given by-

 

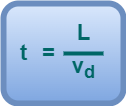
(Equation-02)

 

We know, Electric Current is defined as the rate of flow of charge through the conductor i.e.

 

 

Substituting Equations (1) and (2) here, we get-

 

 

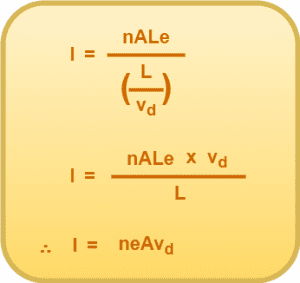
Thus, the relation between electric current and drift velocity is-

 

(Equation-03)

where-

• n = free electron density
• e = charge on electron
• A = area of cross-section of the conductor
• V_d = drift velocity

 

Relation Between Electric Current and Relaxation Time-

 

From Equation-03, the relation between electric current and drift velocity is-

 

(Equation-03)

 

Also, we know the relation between drift velocity and relaxation time is-

 

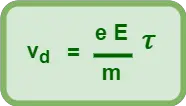
(Equation-04)

 

Also Read- Deriving Relation Between Drift velocity & Relaxation time

 

Using Equation-04 in Equation-03, we get-

 

 

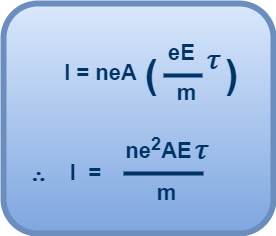
Thus, the relation between electric current and relaxation time is-

 

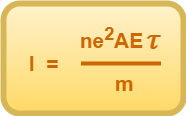
(Equation-05)

 

where-

• n = free electron density
• e = charge on electron
• A = area of cross-section
• E = electric field intensity
• T = relaxation time
• m = mass of electron

 

Deduction of Ohm’s Law-

 

From Equation-05, we have-

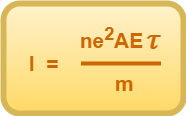
(Equation-05)

 

If V is the potential difference applied across the two ends of the conductor of length L, then electric field inside the conductor is given by-

 

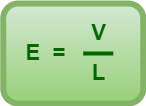
(Equation-06)

 

Using Equation-06 in Equation-05, we get-

 

 

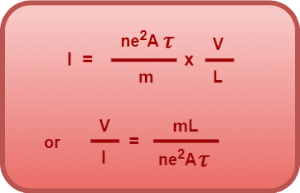
At a fixed temperature, the quantities m, L, n, e, A and T, all have constant values for a given conductor. Therefore,

 

This proves Ohm’s law for a conductor.

 

Here,

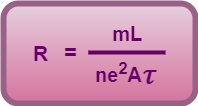
(Equation-07)

R is called as resistance of the conductor.

 

Relation Between Resistivity and Relaxation Time-

 

From Equation-07, we have-

 

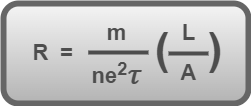
(Equation-07)

 

Also we know, the resistance R of a conductor having length L, cross-sectional area A and resistivity ρ is given by-

 

(Equation-08)

 

On comparing Equation-07 and Equation-08, we get-

 

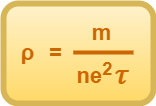
This is the relation between resistivity and relaxation time.

 

Important Note The resistivity of material of the conductor is independent of the dimensions of the conductor. But it depends upon the following two parameters- Free electron density of the conductor Relaxation time

 

Test Your Concepts-

Quiz on Relation Between Electric Current & Drift Velocity

 

Next Article-

Mobility of Charge Carriers

 

Get more notes & other study material of the Chapter Current Electricity.