Ohm’s Law-

 

Before you go through this article, make sure that you have gone through the previous article on Ohm’s law.

 

We have learnt-

• Ohm’s law states that the potential difference applied across the ends of a conductor is directly proportional to the current flowing through it.
• It holds good when the physical conditions such as temperature, pressure etc remains unchanged,

 

In this article, we will learn about Kirchhoff’s Laws.

 

Kirchhoff’s Laws-

 

In 1942, a German physicist Kirchhoff extended Ohm’s law to complicated circuits and gave two laws which enable us to determine current in any part of such a circuit. These laws are called as Kirchhoff’s laws.

 

Kirchhoff gave the following two laws-

 

 

1. Kirchhoff’s Current Law or KCL or Junction Rule

2. Kirchhoff’s Voltage Law or KVL or Loop Rule

 

These laws are discussed below one by one.

 

Kirchhoff’s Current Law-

 

Kirchhoff’s Current Law or KCL states that-

 

In an electric circuit, the algebraic sum of currents at any junction is zero.

 

Mathematically, this law can be expressed as-

 

 

Sign Convention-

 

The following sign convention is followed for applying Kirchhoff’s current law-

• The currents flowing towards the junction are taken as positive.
• The currents flowing away from the junction are taken as negative.

 

Example-

 

The following figure represents a junction in a circuit where four currents meet-

 

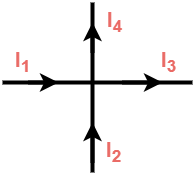
Here,

• The currents I₁ and I₂ are flowing towards the junction.
• The currents I₃ and I₄ are flowing away from the junction.

 

Now, using KCL, we have-

∑I = 0

I₁ + I₂ – I₃ – I₄ = 0

I₁ + I₂ = I₃ + I₄

i.e. incoming current = outgoing current

 

From here, we conclude that Kirchhoff’s current law can also be stated as-

 

The sum of currents entering a junction is equal to the sum of currents leaving that junction.

 

Since Kirchhoff’s current law is applied at any junction of the circuit, it is also called as Junction rule.

 

Justification-

 

Kirchhoff’s current law is based on the law of conservation of charge.

 

This is because when a steady current flows in the circuit, charges cannot accumulate or originate at any point of the circuit. So, whatever charge flows towards the junction in any time interval, an equal charge must flow away from that junction in the same time interval.

 

Kirchhoff’s Voltage Law-

 

Kirchhoff’s Voltage Law or KVL states that-

 

Around any closed loop of a network, the algebraic sum of changes in potential must be zero. OR The algebraic sum of the emfs in any loop of a circuit is equal to the sum of the products of currents and resistances in it.

 

Mathematically, this law can be expressed as-

 

OR

 

Sign Convention-

 

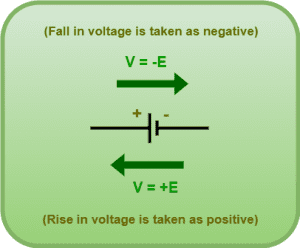
The following sign convention is followed for applying Kirchhoff’s voltage law-

• The loop can be traversed in any direction either clockwise or anticlockwise.
• The emf of cell is taken as positive if the direction of traversal is from its negative to the positive terminal.
• The emf of cell is taken as negative if the direction of traversal is from its positive to the negative terminal.

 

 

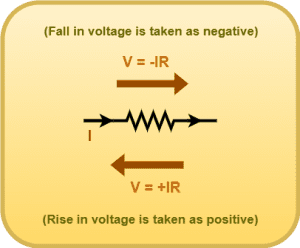
• The IR product is taken as positive if the resistor is traversed in the opposite direction of assumed current.
• The IR product is taken as negative if the resistor is traversed in the same direction of assumed current.

 

 

Since Kirchhoff’s voltage law is applied around any closed loop of the circuit, it is also called as loop rule.

 

Justification-

 

Kirchhoff’s voltage law is based on the law of conservation of energy.

 

This is because electrostatic force is a conservative force. So, the work done by it along any closed path must be zero.

 

Solving Circuit Problems Using Kirchhoff’s Laws-

 

Following steps are followed to find current in different parts of the circuit using Kirchhoff’s laws-

1. Distribute the current in different parts of the circuit in accordance with Kirchhoff’s current law.
2. Form equations using Kirchhoff’s voltage law for each independent loop in the circuit.
3. The number of equations formed will always be equal to the number of variables introduced.
4. Solve the equations so formed to calculate the values of current in different parts of the circuit.

 

Important Notes-

 

On solving the equations,

• If the value of current comes out to be positive, then the assumed direction of current is correct.
• If the value of current comes out to be negative, then the actual direction of current is opposite to the assumed direction.

 

Test Your Concepts-

Quiz on Kirchhoff’s Laws

 

Next Article-

Series Combination of Resistors

 

Get more notes & other study material of the Chapter Current Electricity.