Wheatstone Bridge-

 

In 1843, a British physicist Sir Charles F. Wheatstone suggested a method to determine the value of an unknown resistance.

 

A Wheatstone Bridge is an arrangement of four resistances used to determine one of these resistances quickly and accurately in terms of the remaining three resistances.

 

Construction & Working-

 

• A Wheatstone bridge consists of four resistances P, Q, R and S.
• These resistances are connected to form the arms of a quadrilateral ABCD.
• A battery of emf E is connected between the points A and C.
• A sensitive galvanometer is connected between the points B and D.

 

A Wheatstone bridge is shown in the following diagram-

 

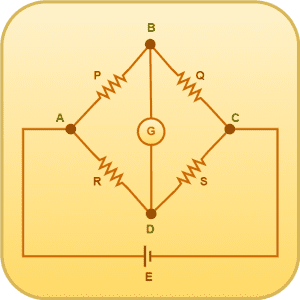
WHEATSTONE BRIDGE

 

Let S be the resistance to be measured.

The resistance R is so adjusted that there is no deflection in the galvanometer.

 

Balanced Condition-

 

The bridge is said to be balanced when the potential difference across the galvanometer is zero so that there is no current flowing through the galvanometer.

 

In the balanced condition of the bridge, we have-

 

 

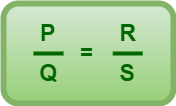
From here, the unknown resistance S is given by-

 

 

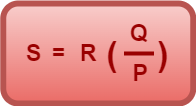
Knowing the ratio of resistances P and Q and the resistance R, we can determine the unknown resistance S.

 

Deriving Balanced Condition of Wheatstone Bridge-

 

In accordance with the Kirchhoff’s current law, the currents through various branches of the Wheatstone bridge are shown-

 

 

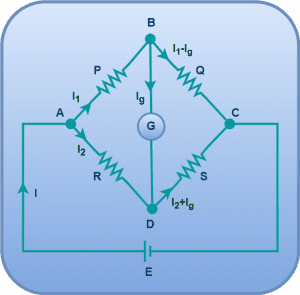
Using Kirchoff’s Voltage Law in the loop ABDA, we have-

 

-I₁P – I_gG + I₂R = 0       ………..(1)

 

Using Kirchoff’s Voltage Law in the loop BCDB, we have-

 

-(I₁ – I_g)Q + (I₂ + I_g)S + I_gG = 0       ………..(2)

 

Also Read- How to Apply Kirchhoff’s Laws?

 

In the balanced condition of the bridge, I_g = 0. Then, the above equations become-

 

-I₁P + I₂R = 0     or     I₁P = I₂R       ………..(3)

-I₁Q + I₂S = 0     or     I₁Q = I₂S       ………..(4)

 

On dividing Equations-03 and 04, we get-

 

 

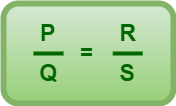
This proves the condition for the balanced Wheatstone bridge.

 

Sensitivity of Wheatstone Bridge-

 

A Wheatstone bridge is said to be sensitive if it shows a large deflection in the galvanometer for a small change of resistance in the resistance arm.

 

The sensitivity of the Wheatstone bridge depends on the following two factors-

• Relative magnitudes of the resistances in the four arms of the bridge. The bridge is most sensitive when all the four resistances are of the same order.
• Relative positions of battery and galvanometer.

 

Advantages of Wheatstone Bridge-

 

The Wheatstone bridge method has the following advantages over other methods for measuring unknown resistance-

• It is a null method. Hence, the internal resistance of the cell and the resistance of the galvanometer do not affect the null point.
• As the method does not involve any measurement of current and potential difference, so the resistances of ammeters and voltmeters do not affect the measurements.
• The unknown resistance can be measured to a very high degree of accuracy.

 

Test Your Concepts-

Quiz on Wheatstone Bridge

 

Next Article-

Meter Bridge

 

Get more notes & other study material of the Chapter Current Electricity.