Combination of Resistors-

 

Before you go through this article, make sure that you have gone through the previous article on Series Combination of Resistors.

 

Sometimes, a number of resistors are connected in a circuit in order to get a desired value of current in the circuit.

 

Resistors may be combined in a circuit in the following ways-

 

 

1. Series Combination
2. Parallel Combination
3. Mixed Combination

 

In this article, we will learn about parallel combination of resistors.

 

Parallel Combination of Resistors-

 

Two or more resistors are said to be connected in parallel combination when- all the resistors are connected between two common points the potential difference across each resistor is same

 

Expression For Equivalent Resistance-

 

Consider-

• Two resistors of resistances R₁ and R₂ are connected in parallel combination across a battery.
• The battery maintains a potential difference V across the combination.

 

 

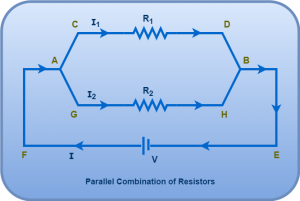
Using Kirchoff’s Voltage Law in the loop ACDBEFA, we have-

 

-I₁R₁ + V = 0

V = I₁R₁

I₁ = V / R₁       ………..(1)

 

Using Kirchoff’s Voltage Law in the loop AGHBEFA, we have-

 

-I₂R₂ + V = 0

V = I₂R₂

I₂ = V / R₂       ………..(2)

 

Also Read- How to Apply Kirchhoff’s Laws?

 

Adding Equations-01 & 02, we get-

 

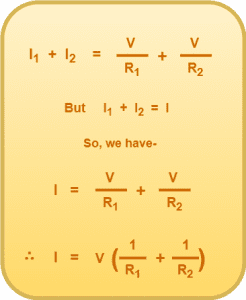
(Equation-03)

 

Now, we wish to replace the above parallel combination of resistors with a single equivalent resistor of resistance R_eq.

 

An equivalent resistor is one which draws the same current from the battery as drawn by the individual resistors together.

 

Replacing the above parallel combination of resistors with an equivalent resistor, we have-

 

 

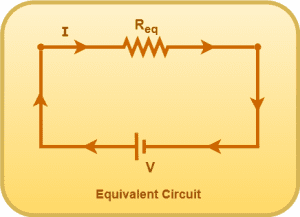
Using Kirchoff’s Voltage Law in the above circuit, we have-

 

-IR_eq + V = 0

V = IR_eq

I = V / R_eq         ………..(4)

 

On comparing equations (3) and (4), we get-

 

 

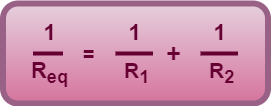
This is the required expression for equivalent resistance of a parallel combination of two resistors.

The formula can be extended for n resistors in the same way.

 

In parallel combination, the reciprocal of equivalent resistance is equal to the sum of reciprocals of the individual resistances.

 

Important Notes-

 

Note-01:

 

In parallel combination,

• The potential difference across each resistor is same but current divides among the individual resistors.
• The total current drawn from the battery is equal to the sum of currents flowing through the individual resistors.

 

Note-02:

 

If two resistors having resistances R₁ and R₂ are combined in parallel combination, then their equivalent resistance is given by-

 

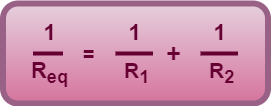
(Not Recommended to Use)

 

Taking LCM and then reciprocal, this formula for two resistors can be rewritten as-

 

(Recommended to Use)

 

Trick To Learn Equivalent Resistance = Product of two resistors / Sum of two resistors

 

If the resistance of one resistor is n times the resistance of the other resistor i.e. R₂ = nR₁ (say), then substituting in the above formula and solving, the formula can be rewritten as-

 

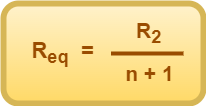
(Recommended to Use)

 

Trick To Learn Equivalent Resistance = Big One / (n+1)

 

Note-03:

 

If n resistors each of resistance R are combined in parallel combination, then their equivalent resistance is given by-

 

 

Note-04:

 

In parallel combination, the equivalent resistance is smaller than the smallest individual resistance.

 

Note-05:

 

The smallest value of equivalent resistance that can be obtained with the given resistances is by combining them in parallel combination.

 

Test Your Concepts-

Quiz on Parallel Combination of Resistors

 

Next Article-

Wheatstone Bridge

 

Get more notes & other study material of the Chapter Current Electricity.