Electric Cell-

 

Before you go through this article, make sure that you have gone through the previous article on Electric Cell.

 

We have learnt-

• An electric cell is a device which supplies energy to the charge carriers and maintain their flow in the electric circuit.
• An ideal cell has zero internal resistance whereas a practical cell has some finite internal resistance.

 

In this article, we will learn about Series Combination of Cells.

 

Combination of Cells-

 

• A single cell provides a feeble current.
• In order to get a higher current in the circuit, we use a combination of cells.

 

A combination of cells is called a battery.

 

Cells may be combined together in the following ways-

 

 

1. Series Combination
2. Parallel Combination
3. Mixed Combination

 

In this article, we will learn about series combination of cells.

 

Series Combination of Cells-

 

The cells are said to be connected in series combination when the negative terminal of the first cell is connected to the positive terminal of the second cell and so on.

 

Expression For Equivalent EMF-

 

Consider two cells having emfs E₁ and E₂ and internal resistances r₁ and r₂ respectively are connected in series combination across an external resistance R as shown-

 

 

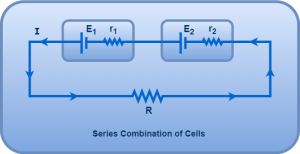
Using Kirchoff’s Voltage Law in the above circuit, we have-

 

-E₁ + Ir₁ – E₂ + Ir₂ + IR = 0

I(r₁ + r₂ + R) = E₁ + E₂

I = (E₁ + E₂) / (r₁ + r₂ + R)         ………..(1)

 

Also Read- How to Apply Kirchhoff’s Laws?

 

Now, we wish to replace the above series combination of cells with a single equivalent cell of emf E_eq and internal resistance r_eq.

 

An equivalent cell is one which supplies the same current to the external resistor as supplied by the individual cells together.

 

Replacing the above series combination of cells with an equivalent cell, we have-

 

 

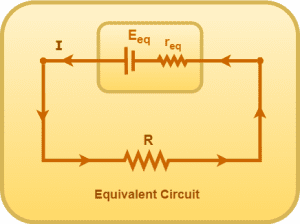
Using Kirchoff’s Voltage Law in the above circuit, we have-

 

-E_eq + Ir_eq + IR = 0

I(r_eq + R) = E_eq

I = E_eq / (r_eq + R)         ………..(2)

 

On comparing equations (1) and (2), we get-

 

 

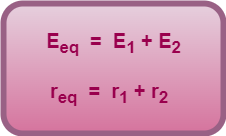
This is the required expression for equivalent emf & internal resistance of a series combination of two cells.

The formula can be extended for n cells in the same way.

 

Important Notes-

 

Note-01:

 

The equivalent emf of a series combination of cells is equal to the sum of their individual emfs.

 

 

Note-02:

 

The equivalent internal resistance of a series combination of cells is equal to the sum of their individual internal resistances.

 

 

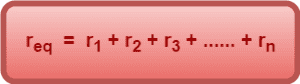
Note-03:

 

The above expression for calculation of equivalent emf is valid only when all the cells assist each other.

If one cell of emf E₂ (say) is turned around, then-

 

 

Note-04:

 

If n identical cells each of emf E and internal resistance r are combined in series combination, then-

 

 

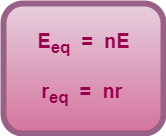
Note-05:

 

If n identical cells each of emf E and internal resistance r are combined in series combination and polarity of m cells is reversed, then-

 

 

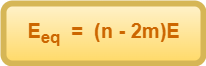
However, the equivalent internal resistance still remains the same i.e. nr.

 

Test Your Concepts-

Quiz on Series Combination of Cells

 

Next Article-

Parallel Combination of Cells

 

Get more notes & other study material of the Chapter Current Electricity.