Electric Potential | Thin Spherical Shell

Electric Potential-

 

Before you go through this article, make sure that you have gone through the previous articles on-

• Electric Field Due To A Charged Thin Spherical Shell
• Relation Between Electric Field & Electric Potential

 

We have learnt-

The electric field due to a charged thin spherical shell is given by-

 

 

The relation between electric field and electric potential is given by-

 

 

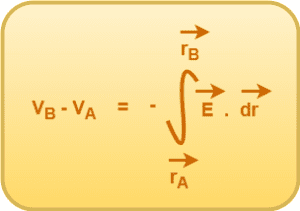
In this article, we will learn about electric potential due to a charged thin spherical shell.

 

Electric Potential Due To A Charged Thin Spherical Shell-

 

Consider a positive charge Q uniformly distributed on the surface of a spherical shell of radius R.

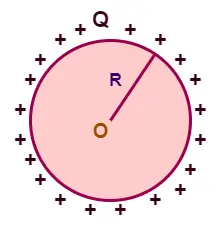
We wish to calculate the electric potential due to a charged thin spherical shell.

 

There are following three cases possible-

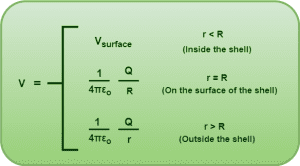
1. When observation point lies outside the shell i.e. r > R
2. When observation point lies on the surface of shell i.e. r = R
3. When observation point lies inside the shell i.e. r < R

 

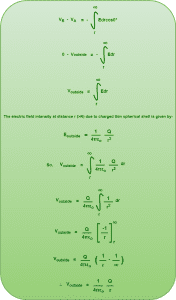
Case-01: When observation point lies outside the shell (r>R)

 

We choose two points-

• The first point say ‘A’ is chosen outside the shell at a distance ‘r’ from the center of shell.
• The second point say ‘B’ is chosen at infinity.

 

We travel from point A to point B and write the relation between electric field and electric potential.

 

Using the relation, we have-

 

 

Substituting the values we have-

 

 

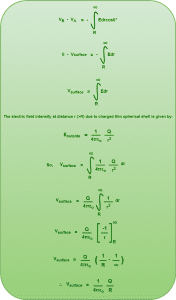
Case-02: When observation point lies on the surface of the shell (r=R)

 

We choose two points-

• The first point say ‘A’ is chosen on the surface of the shell.
• The second point say ‘B’ is chosen at infinity.

 

We travel from point A to point B and write the relation between electric field and electric potential.

 

Using the relation, we have-

 

 

Substituting the values we have-

 

 

Case-03: When observation point lies inside the shell (r<R)

 

We choose two points-

• The first point say ‘A’ is chosen inside the shell.
• The second point say ‘B’ is chosen at infinity.

 

We travel from point A to point B and write the relation between electric field and electric potential.

 

Using the relation, we have-

 

 

Substituting the values we have-

 

 

Important Note It is interesting to note that the electric potential inside the spherical shell at any point is same as the electric potential on its surface.

 

Based on the above discussion, the electric field due to charged thin spherical shell can be summarized as-

 

 

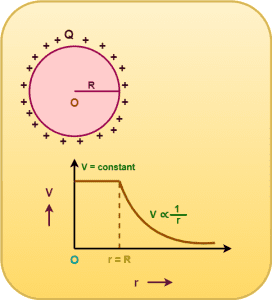
Graph-

 

The following graph shows the variation of electric field intensity due to a charged thin spherical shell with distance from its center-

 

 

Read the next article on-

Equipotential Surface & Its Properties

 

Get more notes & other study material of the Chapter Electrostatic Potential & Capacitance.